数据结构与算法-归并排序教程版

原理介绍

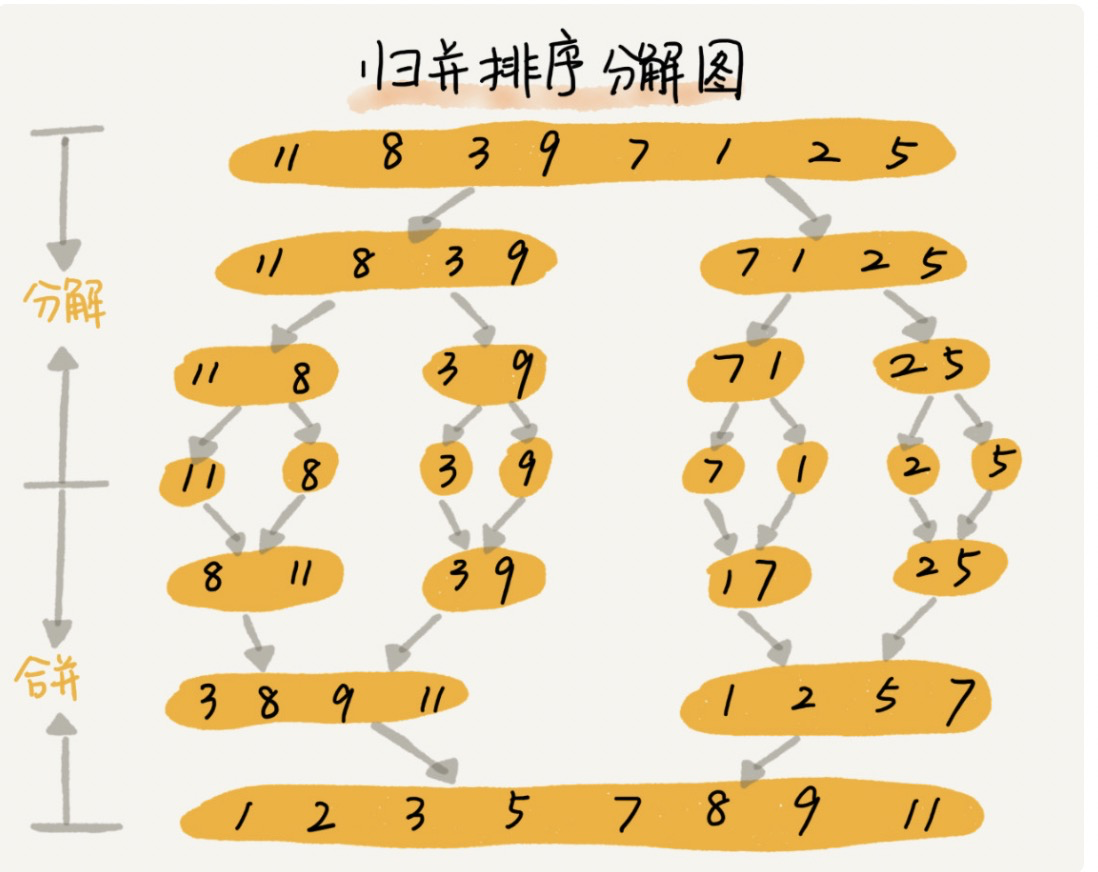
归并排序 其实思想很简单，如上图，就是将待排序数组，分成若干个小数组，将最终的两个数据排序后，在进行合并。简而言之，就是分而治之的思想。将一个大问题，分成若干个小问题来解决，小问题解决了之后，随之大问题也就会迎刃而解。其实分治思想跟递归思想很相像，分析递推公式，找到终止条件，然后根据这个思路进行编码。

代码实现

归并排序的主方法，将待排序数据以及大小传递到核心排序算法方法中。

 // 归并排序算法, a是数组，n表示数组大小
    public static void mergeSort(int[] a, int n) {
        mergeSortInternally(a, 0, n - 1);
    }

如下的递归函数方法，首先是判断终止条件，如果递归调用到数组的最后一位，就会终止调用。我们可以很清楚的看到代码第9、10行是将当前数组分割为两个范围来进行排序，然后进行递归调用当前方法，其实现逻辑就是上面归并排序图的步骤。

 // 递归调用函数
    private static void mergeSortInternally(int[] a, int p, int r) {
        // 递归终止条件
        if (p >= r) return;

        // 取p到r之间的中间位置q,防止（p+r）的和超过int类型最大值
        int q = p + (r - p) / 2;
        // 分治递归
        mergeSortInternally(a, p, q);
        mergeSortInternally(a, q + 1, r);

        // 将A
和A[q+1...r]合并为A

        merge(a, p, q, r);
    }

最后，我们来看下merge这个方法，它其实就是将最终排好序的数据合并成一个有序的数组，并且放入int[] a当中。
具体过程就是，我们申请一个临时数组，与原数组空间已知，使用两个变量i和j，它俩分别指向p和p+1的第一个元素，然后循环当前数据下标，直到数组对比完毕。比较的过程就是如果a[i] <= a[j]时，将a[i]放入临时数组中，并且i后移一位，否则将a[j]放入临时数组中，并且j后移一位。循环对比，直到其中一个数组中的数据都放入了临时数组当中，再将另一个数组中的数据追加到第一个数组末尾，这个时候两个已排序后的数据就合并完成了。最后将临时数组中的数据拷贝到int a[]数组中即可。

 // 递归调用函数
    private static void mergeSortInternally(int[] a, int p, int r) {
        // 递归终止条件
        if (p >= r) return;

        // 取p到r之间的中间位置q,防止（p+r）的和超过int类型最大值
        int q = p + (r - p) / 2;
        // 分治递归
        mergeSortInternally(a, p, q);
        mergeSortInternally(a, q + 1, r);

        // 将A
和A[q+1...r]合并为A

        merge(a, p, q, r);
    }

    private static void merge(int[] a, int p, int q, int r) {
        int i = p;
        int j = q + 1;
        int k = 0; // 初始化变量i, j, k
        int[] tmp = new int[r - p + 1]; // 申请一个大小跟a
一样的临时数组
        while (i <= q && j <= r) {
            if (a[i] <= a[j]) {
                tmp[k++] = a[i++]; // i++等于i:=i+1
            } else {
                tmp[k++] = a[j++];
            }
        }

        // 判断哪个子数组中有剩余的数据
        int start = i;
        int end = q;
        if (j <= r) {
            start = j;
            end = r;
        }

        // 将剩余的数据拷贝到临时数组tmp
        while (start <= end) {
            tmp[k++] = a[start++];
        }

        // 将tmp中的数组拷贝回a

        for (i = 0; i <= r - p; ++i) {
            a
 = tmp[i];
        }
    }

测试结果

最后写一个测试方法来测试归并排序算法，如下

 int[] mergeSort = {11, 8, 3, 9, 7, 1, 2, 5};
        mergeSort(mergeSort, mergeSort.length);
        for (int i = 0; i < mergeSort.length; i++) {
            System.out.print(mergeSort[i] + " ");
        }

最终排序结果为1 2 3 5 7 8 9 11